In this section, our purpose is to evaluate the radial integrals in the single-particle matrix elements of the multipole operators: 2024.03.28 - [Nuclear Physics/From Nucleons to Nucleus] - 6.1.3 Single-Particle Matrix Elements of the Multipole Operators
6.1.3 Single-Particle Matrix Elements of the Multipole Operators
In this posting, I derive the single-particle matrix elements of the multipole operators. 1. Single particle matrix elements for electric tensor operator ($\sigma = E$) The electric tensor operator is given as \begin{eqnarray} Q_{\lambda \mu} = \zeta^{\rm
djlab.tistory.com
In general, the oscillator function $g_{nl}(r,b)$ is given as
\begin{eqnarray} g_{nl}(r) = \sqrt{\frac{2n!}{b^3 \Gamma(n+l+\frac{3}{2}) }} \left( \frac{r}{b} \right)^l e^{-r^2/2b^2} L_n^{(l+\frac{1}{2})} (r^2/b^2), \label{1}\tag{1} \end{eqnarray}
where $L_n^{(l+ \frac{1}{2})}$ is the associated Laguerre polynomial, and the parameter $b$ is the oscillator length. The oscillator length is given by
$$ b \equiv \sqrt{\frac{\hbar}{m_N \omega}} = \frac{\hbar c}{\sqrt{(m_N c^2)(\hbar \omega)}}.$$
In Eq. (\ref{1}), if we define a dimensionless variable $x \equiv r/b$, then,
\begin{eqnarray} g_{nl}(x,b) = \sqrt{\frac{1}{b^3}} \sqrt{\frac{2n!}{\Gamma(n+l+\frac{3}{2} ) }} x^l e^{-x^2/2} L_n^{(l+\frac{1}{2})} (x^2) \equiv b^{-\frac{3}{2}} \tilde{g}_{nl}(x) \label{2}\tag{2}. \end{eqnarray}
Figure 1 shows examples of $\tilde{g}_{nl}(x)$ as a function of $x$.
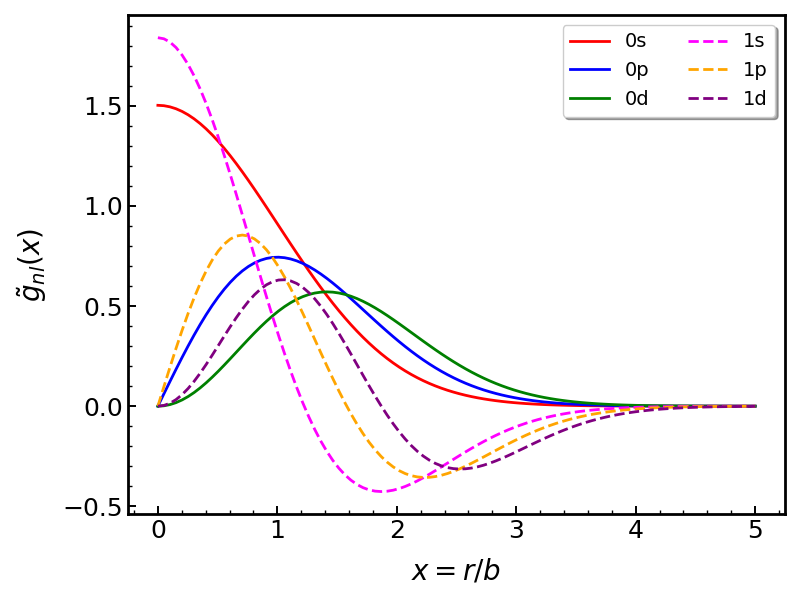
Using $\tilde{g}_{nl}(x)$, one can also rewrite the given radial integral as follows:
\begin{eqnarray} R_{ab}^\lambda &=& \int_0^\infty g_{n_a l_a} (r) r^\lambda g_{n_b l_b}(r) r^2 dr = \int_0^\infty \left( b^{- \frac{3}{2}} \tilde{g}_{n_a l_a} (x) \right) \left( b x \right)^\lambda \left( b^{-\frac{3}{2}} \tilde{g}_{n_b l_b}(x) \right) \left( bx \right)^2 (b dx) \\[12pt] &=& b^\lambda \int_0^\infty \tilde{g}_{n_a l_a} (x) x^{\lambda +2} \tilde{g}_{n_b l_b}(x) dx \equiv b^\lambda \tilde{R}^{(\lambda)}_{ab}. \end{eqnarray}
Although the elegant recursion relation can derive $\tilde{R}^{(\lambda)}_{ab}$ [1], the integral is easily evaluated numerically. Therefore, I omit its detailed derivation. Instead, I provide a simple Python code to compute $\tilde{R}^{(\lambda)}_{ab}$ as follows:
import numpy as np
from scipy.integrate import quad
from scipy.special import factorial, gamma, genlaguerre
# Define tilde_g
def tilde_g(x, n, l):
fac_n = factorial(n)
L_n = genlaguerre(n, l + 0.5)
return np.sqrt(2 * fac_n / gamma(n + l + 1.5)) * (x ** l) * np.exp(-x ** 2 / 2) * L_n(x ** 2)
# Define R functions
def R(n_a, l_a, lam, n_b, l_b):
dRdx = lambda x: tilde_g(x, n_a, l_a) * (x ** (lam + 2)) * tilde_g(x, n_b, l_b)
result, _ = quad(dRdx, 0, np.inf)
return result
# Mapping for l_a, l_b values
l_mapping = {"s": 0, "p": 1, "d": 2, "f": 3}
# Read input for n_a and l_a at the same time
n_a_str, l_a_input = input("Enter the values of n_a and l_a separated by a space (e.g. 0 s): ").split()
n_a = int(n_a_str)
l_a = l_mapping.get(l_a_input.lower(), None)
# If l_a is not found in the mapping
if l_a is None:
print("Invalid input for l_a. Please enter 's', 'p', 'd', or 'f'.")
else:
# Read input for lam, n_b, and l_b
lam = int(input("Enter the value of lambda: "))
n_b_str, l_b_input = input("Enter the values of n_b and l_b separated by a space (e.g. 0 s): ").split()
n_b = int(n_b_str)
l_b = l_mapping.get(l_b_input.lower(), None)
# If l_b is not found in the mapping
if l_b is None:
print("Invalid input for l_b. Please enter 's', 'p', 'd', or 'f'.")
else:
# Calculate and print the result
result = R(n_a, l_a, lam, n_b, l_b)
print("Result: R(n_a={}, l_a={}, lambda={}, n_b={}, l_b={}) = {:.3f}".format(n_a, l_a_input, lam, n_b, l_b_input, result))
After saving this code, one can execute it using the following command:
python [file_name].py
Then, you can enter the variables of $n_a, l_a, \lambda, n_b, l_b$ as follows
Enter the values of n_a and l_a separated by a space (e.g. 0 s): 0 s
Enter the value of lambda: 2
Enter the values of n_b and l_b separated by a space (e.g. 0 s): 0 p
For this example, the result shows
Result: R(n_a=0, l_a=s, lambda=2, n_b=0, l_b=p) = 1.843
Reference
[1] From Nucleons to Nucleus: Concepts of Microscopic Nuclear Theory, Jouni Suhonen, Springer, 2007 (pp. 125-126.)
'Nuclear Physics > From Nucleons to Nucleus' 카테고리의 다른 글
| 6.1.6 Electromagnetic Multipole Moments (0) | 2024.04.11 |
|---|---|
| 6.1.5 Tables of Numerical Values of Single-Particle Matrix Elements (0) | 2024.04.11 |
| 6.1.3 Single-Particle Matrix Elements of the Multipole Operators (0) | 2024.03.28 |
| 6.1.2 Selection Rules for Electromagnetic Transitions (0) | 2024.03.26 |
| Derivation of Eq. (34) in Magnetic tensor operator (0) | 2024.03.20 |



