이번 포스팅에서는 큐비트가 두 개인 경우에 대해 적용 가능한 이진 연산자중에서 SWAP 게이트에 대해 알아보겠습니다.
2큐비트 시스템
2큐비트 시스템은 말 그대로 2개의 큐비트를 갖는 상태를 의미합니다. 하나의 큐비트가 0 또는 1을 가질 수 있으므로, 2 큐비트 상태는 $|00\rangle$, $|01\rangle$, $|1 0\rangle$, $|11\rangle$ 등 총 4개의 상태를 가질 수 있습니다. 이를 행렬로 표현하면 아래와 같습니다:
\begin{eqnarray} |00\rangle = \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}, \ \ \ \ |01\rangle = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix}, \ \ \ \ |10\rangle = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix}, \ \ \ \ |11\rangle = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}. \end{eqnarray}
그럼 이러한 2큐비트 상태에 대한 이진 연산자들에 대해 알아 보겠습니다.
SWAP 연산자
SWAP 연산자는 말그대로 큐비트의 상태를 $|0 1 \rangle$에서 $|1 0 \rangle$로 (혹은 $|1 0 \rangle$을 $|0 1\rangle$로) 바꿔주는 연산자를 말합니다. 이 연산자는 행렬로 아래와 같이 주어집니다:
\begin{eqnarray} {\rm SWAP} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\end{eqnarray}
이러한 연산자를 이용하면 위에서 정의된 $|10\rangle$상태를 $|0 1 \rangle$ 상태로 변경가능합니다:
\begin{eqnarray} {\rm SWAP} | 1 0 \rangle = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} = | 0 1 \rangle. \end{eqnarray}
반대의 경우도 가능합니다:
\begin{eqnarray} {\rm SWAP} | 0 1 \rangle = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix} = | 1 0 \rangle. \end{eqnarray}
Qiskit 예제
그럼 이러한 연산자를 Qiskit을 이용해 구현해 보겠습니다. 우선 2큐비트 상태를 아래와 같은 명령어로 생성합니다:
from qiskit import QuantumCircuit
# 양자 회로 생성
qc = QuantumCircuit(2) # 2개의 큐비트를 가진 회로 생성
생성된 2큐비트 상태는 $|0 0 \rangle$ 상태를 갖습니다. SWAP 연산자를 테스트 하기 위해 0번째 큐비트에 X연산자를 적용해 $|0 \rangle$에서 $|1\rangle$로 바꿔주겠습니다:
qc.x(0)
그럼, 이제 $|1 0\rangle$의 상태를 갖는 2큐비트 상태를 만들었습니다. 나중에 최종 결과와 비교하기 위해, 블로흐 구안에서 준비된 상태를 시각화하면 아래와 같습니다:
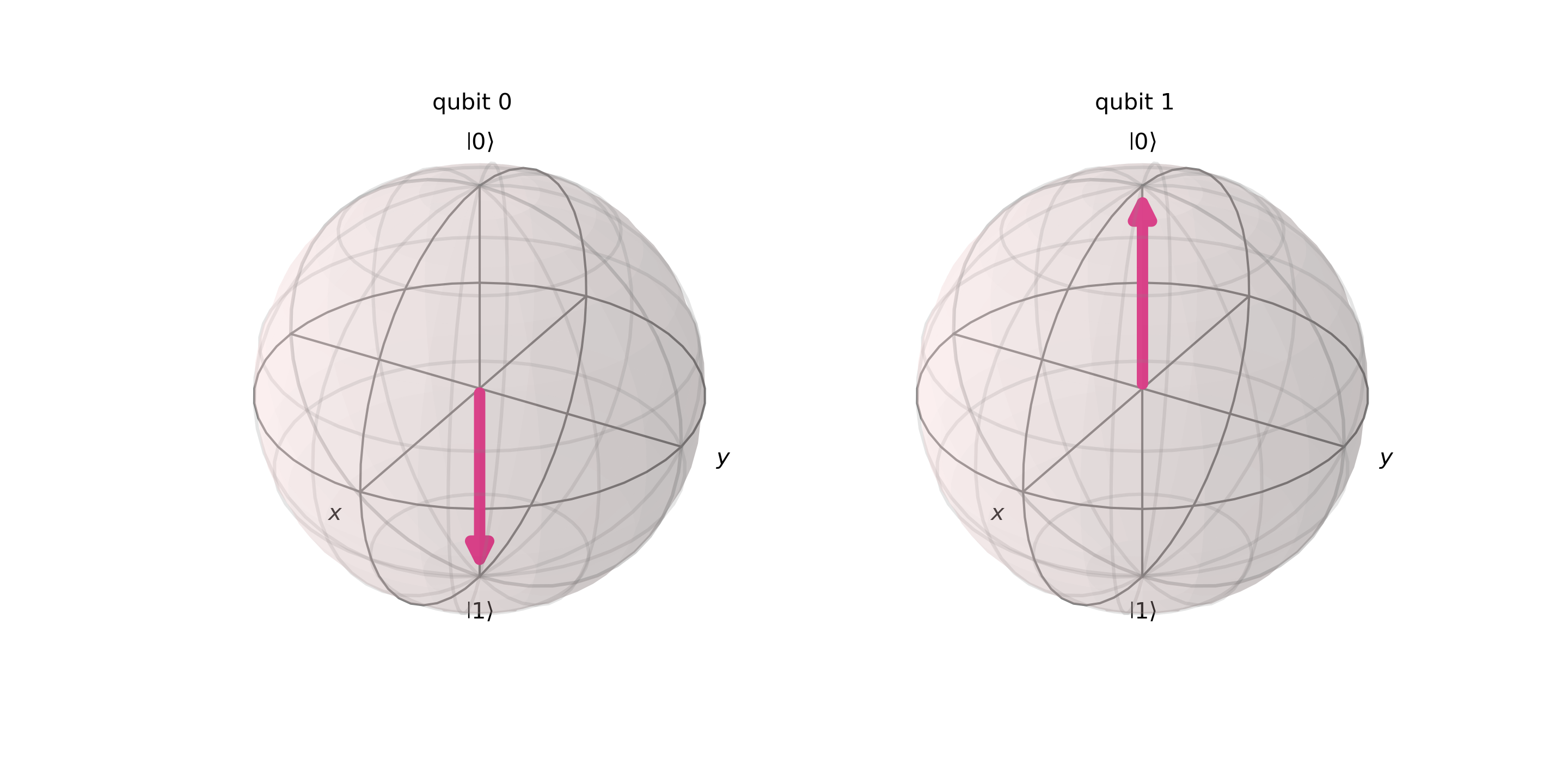
그럼 주어진 상태에 SWAP 연산자를 가해보겠습니다.
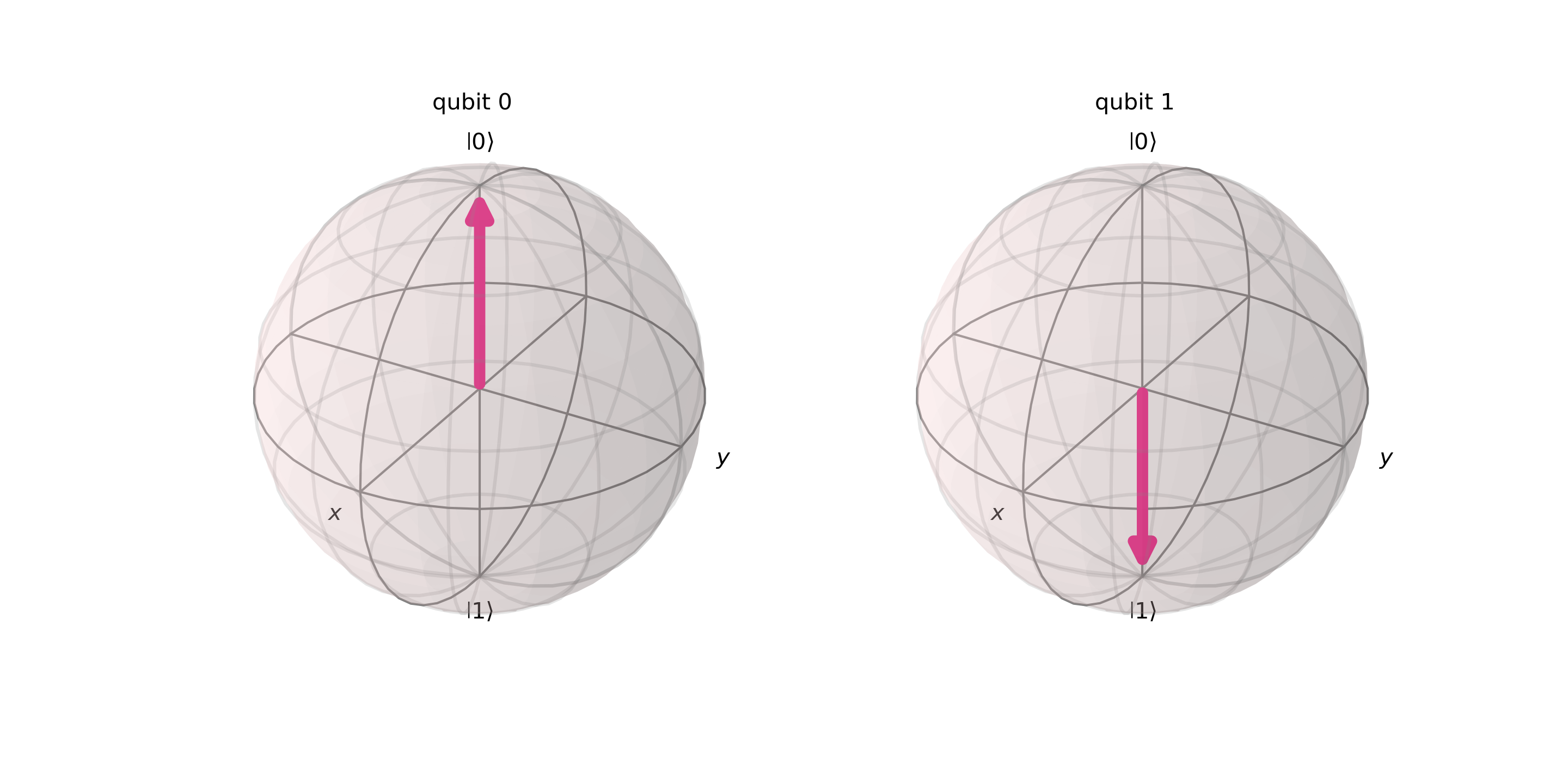
qc.swap(0, 1)이 명령어는 0번 큐비트와 1번 큐비트트 교환하겠다는 뜻입니다. 그럼 결과를 저장하여 최종 상태를 시각화하면 아래와 같이 두 상태가 교환된 것을 볼 수 있습니다!
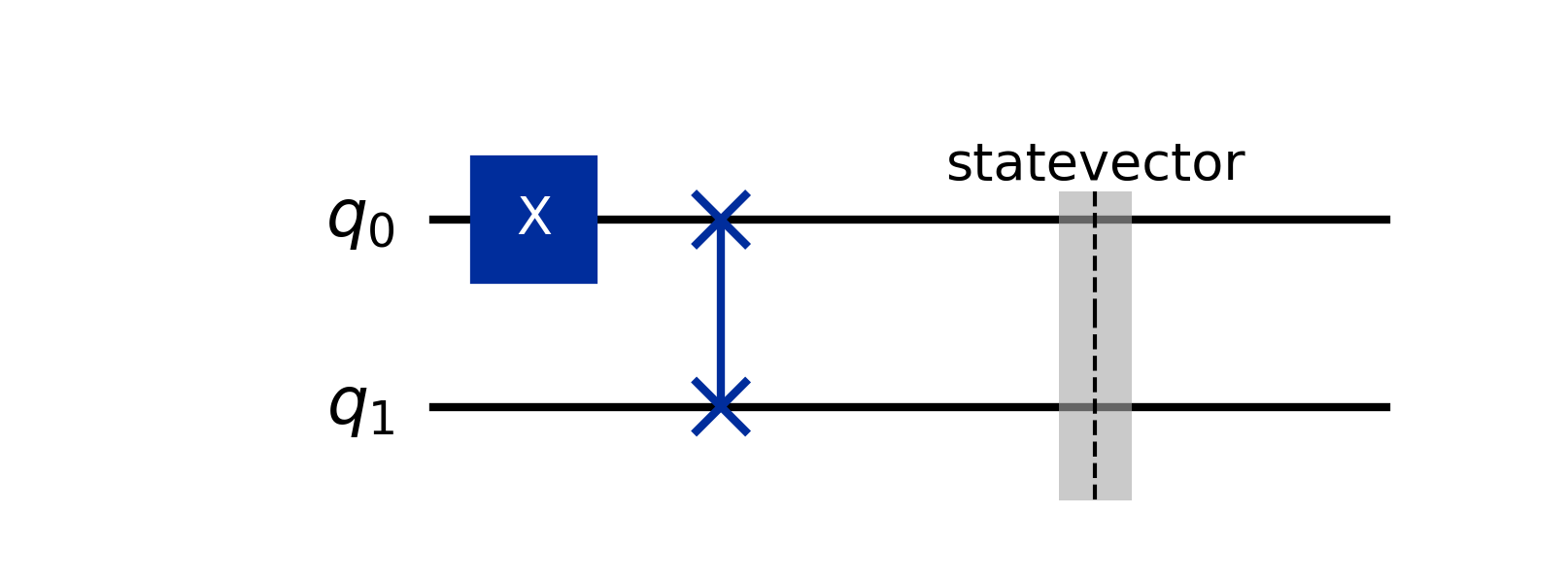
이에 해당하는 양자 회로도 모양은 아래와 같이 표현이 됩니다 (SWAP 게이트의 회로 모양을 기억해 주세요.):
시각화 과정을 포함한 전체 코드는 아래와 같습니다:
from qiskit import QuantumCircuit, transpile
from qiskit.visualization import plot_bloch_multivector, plot_histogram
from qiskit_aer import AerSimulator
import matplotlib.pyplot as plt
# 1. 양자 회로 생성
qc = QuantumCircuit(2) # 2개의 큐비트 생성
# 2. 0번째 큐비트에 Pauli-X 게이트 적용
qc.x(0)
# 3. SWAP 연산자 적용: 0 큐비트 <-> 1 큐비트
qc.swap(0,1)
# 상태 벡터 저장
qc.save_statevector()
# 시뮬레이터 초기화
simulator = AerSimulator()
# 회로 컴파일 및 실행
compiled_circuit = transpile(qc, simulator)
result = simulator.run(compiled_circuit).result()
# 상태 벡터 확인
statevector = result.get_statevector()
print("Statevector:", statevector)
# 상태 시각화
bloch_sphere = plot_bloch_multivector(statevector) # Matplotlib 객체 반환
bloch_sphere.savefig("bloch_sphere.png", dpi=300) # PNG로 저장
# Matplotlib 스타일로 회로 플롯
fig = qc.draw(output="mpl") # Matplotlib 객체 반환
fig.savefig("quantum_circuit.png", dpi=300) # PNG로 저장'Quantum Computing' 카테고리의 다른 글
| Qiskit을 이용한 양자 컴퓨팅 예제 (6) - 양자 상태의 측정 (Measurement) (0) | 2024.12.16 |
|---|---|
| Qiskit을 이용한 양자 컴퓨팅 예제 (5) - 이진 연산자: CNOT, CZ 게이트 (0) | 2024.12.15 |
| Qiskit을 이용한 양자 컴퓨팅 예제 (3) - 아다마르 게이트 (Hadamard Gate) (0) | 2024.12.02 |
| Qiskit을 이용한 양자 컴퓨팅 예제 (2) - 양자회로와 블로흐 구(Bloch Sphere)의 시각화 (0) | 2024.11.27 |
| Qiskit을 이용한 양자 컴퓨팅 예제 (1) - 파울리 게이트(Pauli Gate) (0) | 2024.11.27 |



