이번 포스팅에서는 양자 상태의 측정에 대해 알아보도록 하겠습니다.
고전 물리학에서는 운동 방정식이 정해진다면, 물체의 상태를 정확하게 예측할 수 있습니다. 그렇기 때문에, 측정이라는 행위는 상태에 영향을 미치지 않고 예측과 정확히 일치합니다.
그러나 양자 물리학에서는 입자의 상태가 고전적으로 관측 가능한 상태들의 중첩으로 기술이 되며, 측정을 통해 상태가 결정됩이다. 예를 들면, 어떠한 양자 정보 $|\Psi \rangle$ 상태는 고전적 정보의 상태인 $|0\rangle$ 또는 $|1 \rangle$ 상태를 가질 수 있습니다. 따라서, $|\Psi \rangle$는 아래와 같이 중첩으로 기술이 가능합니다:
\begin{eqnarray} | \Psi \rangle = \alpha |0 \rangle + \beta | 1 \rangle. \end{eqnarray}
여기서 $\alpha^2 + \beta^2 =1$이 됩니다.
그럼 $|\Psi\rangle$로부터 $|0\rangle$ 상태를 관측할 확률은 아래와 같습니다:
\begin{eqnarray} | \langle 0 | \Psi \rangle |^2 = | \alpha \langle 0 | 0 \rangle + \beta \langle 0 | 1 \rangle |^2 = |\alpha|^2 \end{eqnarray}
반면, $|1 \rangle$ 상태를 관측할 확률은 아래와 같습니다:
\begin{eqnarray} | \langle 1 | \Psi \rangle |^2 = | \alpha \langle 1 | 1 \rangle + \beta \langle 1 | 1 \rangle |^2 = |\beta|^2. \end{eqnarray}
이러한 원리를 Qiskit을 이용해 코드로 구현해 보겠습니다.
Qiskit 예제
먼저 두 개의 큐비트를 생성하겠습니다:
qc = QuantumCircuit(2,2)
여기서 QuantumCircuit(2,2)는 2개의 큐비트와 2개의 고전 비트를 생성한다는 뜻입니다. 양자적 상태를 측정하여 얻은 결과를 고전 비트에 저장하기 위해 고전 비트도 함께 생성합니다.
그 다음 0번째 큐비트에 아마다르 게이트를 적용하고, 두 큐비트에 CNOT 게이트를 적용하겠습니다.
qc.h(0) # 첫 번째 큐비트를 중첩 상태로
qc.cx(0, 1) # CNOT 게이트 적용
이를 수식으로 작성하면 아래와 같습니다:
- 0번째 큐비트에 아마다르 게이트 적용(중첩 상태):
\begin{eqnarray} {\bf H} | 0 \rangle = \frac{1}{\sqrt{2}} \left[ |0 \rangle + | 1 \rangle \right] \end{eqnarray} - 두 큐비트에 CNOT 게이트 적용(얽힘 상태):
\begin{eqnarray} \frac{1}{\sqrt{2}} \left[ {\rm CNOT } | 0 0 \rangle + {\rm CNOT} | 1 0 \rangle \right] = \frac{1}{\sqrt{2}} \left[ | 0 0 \rangle + | 1 1 \rangle \right] \end{eqnarray}
이러한 상태를 벨 상태(Bell State)라고 하며, 양자 얽힘(Quantum Entanglement)을 대표적으로 보여주는 예입니다.
위의 예시에서, 첫 번째 큐비트를 $|0\rangle$로 측정하면 두 번째 큐비트도 자동으로 $|0\rangle$ 상태로 결정됩니다. 마찬가지로, 첫 번째 큐비트를 $|1\rangle$로 측정하면 두 번째 큐비트는 $|1\rangle$ 상태로 결정됩니다. 이처럼 하나의 큐비트 상태가 다른 큐비트 상태를 즉시 결정짓는 것은 두 큐비트가 강하게 얽혀 있기 때문입니다.
특히, 두 큐비트를 서로 다른 공간으로 분리해 두어도 이러한 얽힘은 유지됩니다. 두 큐비트가 물리적으로 멀리 떨어져 있어도, 한 큐비트를 측정하는 순간 다른 큐비트의 상태가 즉시 결정됩니다. 이는 양자 물리학의 독특한 현상을 보여주는 대표적인 사례이며, 양자 정보 이론에서 암호화, 통신, 계산 등 다양한 응용에 활용됩니다.
그럼 생성된 큐비트를 측정해 보도록 하겠습니다. 측정에 대한 명령어는 아래와 같습니다:
qc.measure(0,0)
qc.measure(1,1)0번 큐비트를 측정하여 0번 고전 비트에, 1번 큐비트를 측정하여 1번 고전 비트에 저장하겠다는 뜻입니다.
이러한 과정을 양자 회로도로 표현하면 아래와 같습니다:
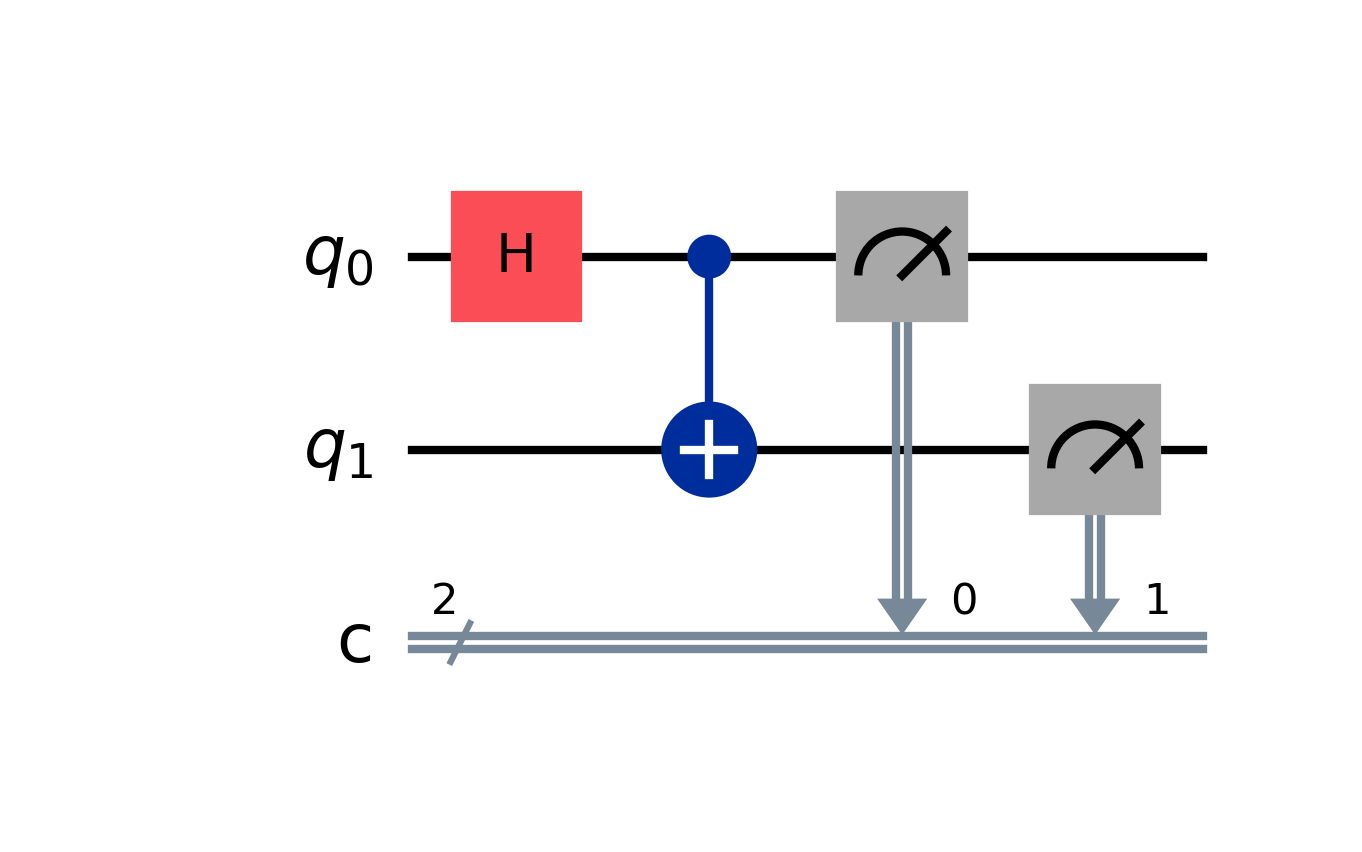
주어진 회로를 100번 시뮬레이션 해보겠습니다:
compiled_circuit = transpile(qc, simulator)
result = simulator.run(compiled_circuit, shots=100).result()
counts = result.get_counts()
print("Counts:", counts)
얻은 결과는 아래와 같습니다: $| 11 \rangle$ 상태는 46번 $| 00 \rangle$ 상태는 54번 측정되었습니다.
Counts: {'11': 46, '00': 54}
이론적으로는 $| 11 \rangle$ 상태와 $|00 \rangle$ 상태를 측정할 확률은 각각 0.5가 되어야 합니다. 그러나 시뮬레이션 결과는 이론값과 약간 차이를 보입니다. 이는 반복 횟수가 충분하지 않기 때문입니다. 위 코드에서 시뮬레이션의 횟수(shots)를 증가시킬수록 두 상태의 측정 확률이 점점 0.5로 수렴할 것입니다.
아래 그림은 각 상태의 측정 확률을 시뮬레이션 횟수에 대해 보여주는 그래프입니다. 시뮬레이션 횟수가 증가할 수록, 두 상태를 측정할 확률이 0.5로 수렴하는 것을 볼 수 있습니다.
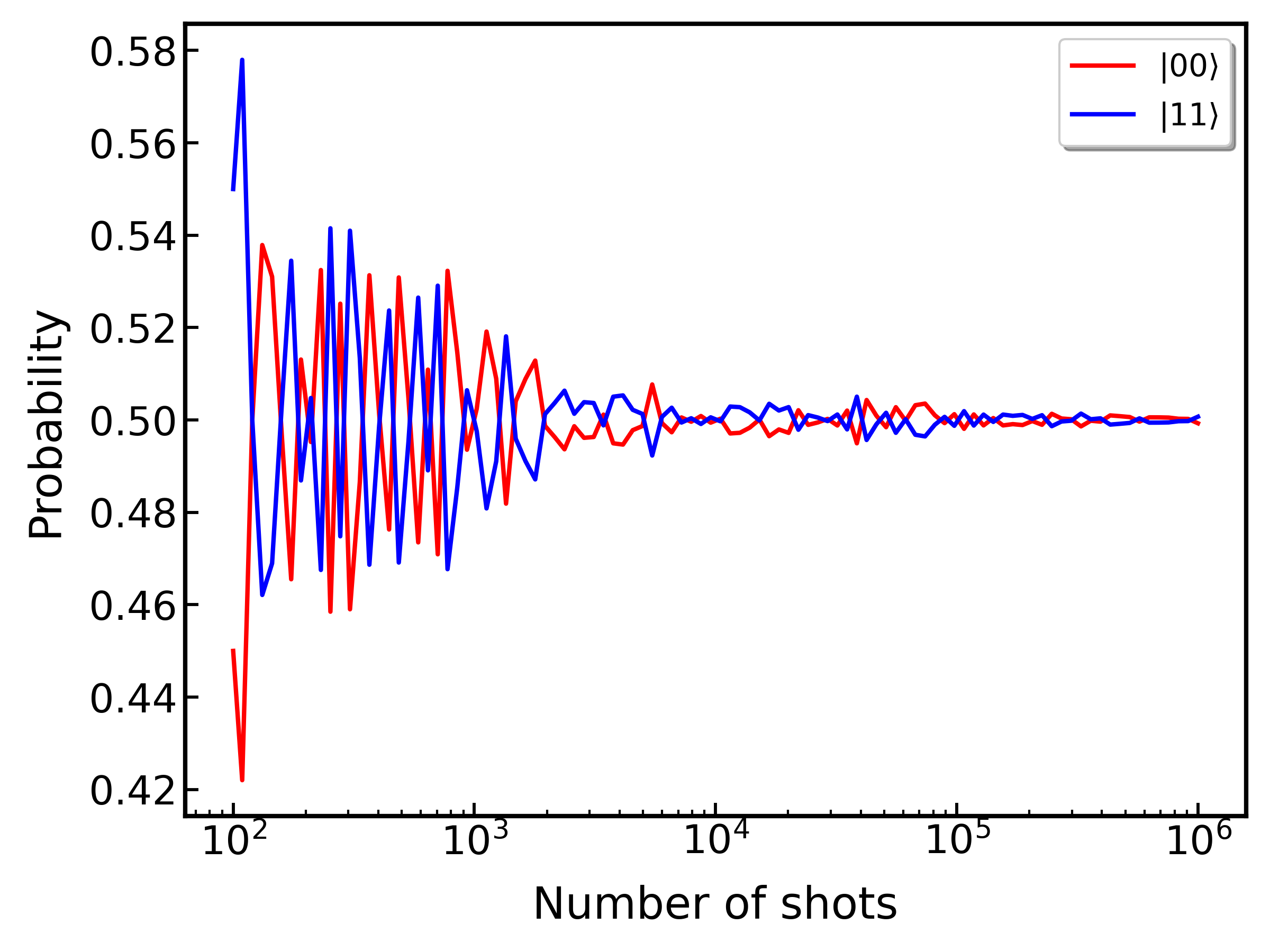
아래는 위 예제에 대한 전체 코드입니다:
from qiskit import QuantumCircuit, transpile
from qiskit.visualization import plot_bloch_multivector, plot_histogram
from qiskit_aer import AerSimulator
import matplotlib.pyplot as plt
# 1. 양자 회로 생성
qc = QuantumCircuit(2,2) # 2개의 큐비트 생성
# 2. 양자 얽힘 만들기
qc.h(0)
qc.cx(0,1)
# 3. 측정
qc.measure(0,0)
qc.measure(1,1)
# 시뮬레이터 초기화
simulator = AerSimulator()
# 회로 컴파일 및 실행
compiled_circuit = transpile(qc, simulator)
result = simulator.run(compiled_circuit, shots=100).result()
counts = result.get_counts()
print("Counts:", counts)
# Matplotlib 스타일로 회로 플롯
fig = qc.draw(output="mpl") # Matplotlib 객체 반환
fig.savefig("quantum_circuit.png", dpi=300) # PNG로 저장
'Quantum Computing' 카테고리의 다른 글
| Qiskit 예제 - 양자 위상 추정 (Quantum Phase Estimation, QPE) (0) | 2025.01.13 |
|---|---|
| Qiskit을 이용한 양자 컴퓨팅 예제 (7) - 양자 푸리에 변환 (Quantum Fourier Transform) (1) | 2024.12.30 |
| Qiskit을 이용한 양자 컴퓨팅 예제 (5) - 이진 연산자: CNOT, CZ 게이트 (0) | 2024.12.15 |
| Qiskit을 이용한 양자 컴퓨팅 예제 (4) - 이진 연산자: SWAP 게이트 (0) | 2024.12.15 |
| Qiskit을 이용한 양자 컴퓨팅 예제 (3) - 아다마르 게이트 (Hadamard Gate) (0) | 2024.12.02 |



