이번 포스팅에서는 허용된 베타 붕괴(Allowed Beta Decay)의 반감기와 ft value에 대해 알아보도록 하겠습니다.
지난번 포스팅에서 마지막 결과식을 다시 보도록 하겠습니다:
$$T_{fi} = \int T_{fi}(p_e) dp_e = \frac{m_e^5 c^4}{2\pi^3 \hbar^7} f(Z, E_0) | \sum_{\mu M_f} \langle \xi_f J_f \, M_f | {\pmb O}_{\lambda \mu} | \xi_i \, J_i \, M_i \rangle |^2. $$
여기서 Matrix element 식은 아래와 같이 Wigner-Eckart 정리를 이용하여 reduced matrix elements의 형태로 적을 수 있습니다:
\begin{eqnarray} \sum_{\mu M_f} \langle \xi_f J_f \, M_f | {\pmb O}_{\lambda \mu} | \xi_i \, J_i \, M_i \rangle |^2 &=& \sum_{\mu M_f} \left| (-1)^{J_f - M_f} \begin{pmatrix} J_f & \lambda & J_i \\ - M_f & \mu & M_i \end{pmatrix} ( \xi_f J_f || {\pmb O}_{\lambda} || \xi_i \, J_i ) \right|^2 \\[12pt] &=& \frac{1}{2J_i + 1} | ( \xi_f J_f || {\pmb O}_{\lambda} || \xi_i \, J_i ) |^2 \end{eqnarray}
그럼 연산자의 형태가 구체적으로 어떤 모양을 갖는 지에 대해서 알아보겠습니다.
지난 포스팅에서 설명한 것처럼, 핵의 베타 붕괴는 아래와 같은 파인먼 다이어그램으로 기술이 가능하며, W-보존의 질량이 핵 에너지 보다 매우 크기 때문에 contact interaction으로 근사가 가능합니다:
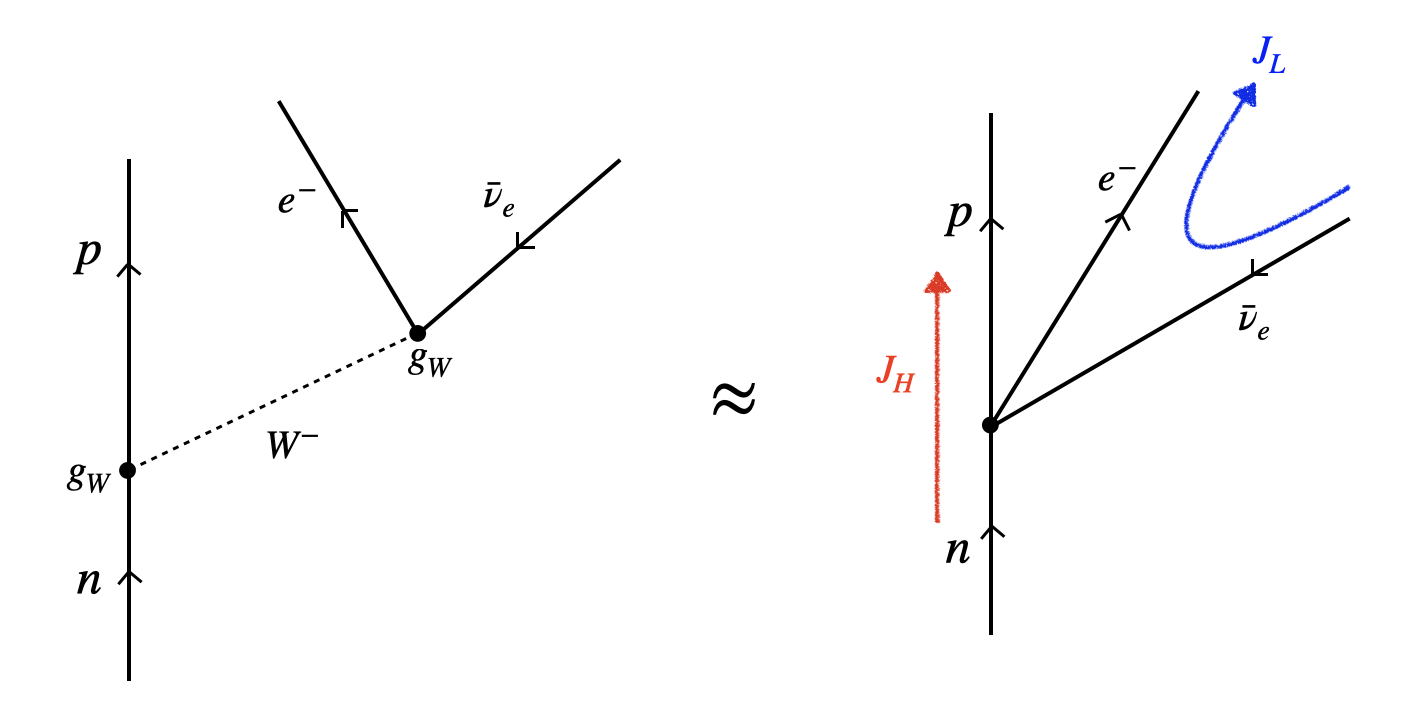
자유 공간에서의 중성자의 베타 붕괴를 기술할 때, 그림에서 주어진 nuclear current $J_H$는 아래와 같은 형태로 기술이 가능합니다:
$$ J_H^\mu = \bar{\Psi}_p(x) \gamma^\mu (C_V + C_A \gamma^5) \Psi_n(x). $$
여기서 $C_V$는 Vector 항과 관련된 결합 상수이며, $C_A$는 axial vector 항과 관련된 결합 상수입니다.
베타 붕괴가 일어날 때, 방출되는 경입자들에 의한 반동으로 인해 핵자는 살짝 밀려나게 될 것입니다. 그러나 이러한 에너지는 수 MeV인데 반해, 핵자의 질량은 약 1 GeV 정도로 매우 큽니다. 결국 핵자의 파동 함수를 기술하는 데 있어, 우리는 비상대론적 근사를 사용할 수 있습니다. 비상대론적 근사에 의해, 핵자의 파동함수는 아래와 같이 기술이 가능합니다:
$$ \Psi_i({\pmb x}) \approx \begin{pmatrix} \chi_i({\pmb x}) \\ 0 \end{pmatrix} $$
이에 따라 주어진 nuclear current 에서 vector 항과 axial vector 항은 각각 아래와 같이 쓰여질 것입니다:
$$ \bar{\Psi}_p \gamma^\mu \Psi_n \approx \chi^\dagger_p \chi_n, \ \ \ \bar{\Psi}_p {\pmb \gamma} \gamma_5 \Psi_n \approx \chi_p^\dagger {\pmb \sigma} \chi_n.$$
(좀 더 자세한 유도를 보고 싶으시다면, W. Greinger의 책 [Gauge Theory of Weak Ineractions]의 Exercise 1.3을 참고하시면 좋습니다.)
이러한 중성자 한 개가 베타붕괴하는 과정의 current 식으로부터 위에 주어진 연산자의 형태를 추정할 수가 있습니다. Vector 항과 관련해서는 항등 연산자 ${\pmb 1}$이, Axial-vector 항에 대해서는 ${\pmb \sigma}$가 작용한다는 것을 알 수 있습니다. 그러나, 실제로 우리의 관심사는 핵자 하나가 아니라, 여러 핵자들이 뭉쳐있는 핵의 베타 붕괴입니다. 여러 핵자로 구성된 핵의 파동 함수의 초기 상태를 $| \xi_i \, J_i \, M_i \rangle$로, 최종 상태를 $| \xi_f \, J_f \, M_f \rangle$라고 하겠습니다. 그러면 위에 주어진 연산자를 이 두 핵자 사이에 작용시킨다면, 위에서 주어진 reduced matrix element를 아래와 같이 적을 수 있을 것입니다:
\begin{eqnarray} \sum_{\mu M_f} | \langle \xi_f \, J_f \, M_f | {\pmb O}_{\lambda \mu } | \xi_i \, J_i \, M_i \rangle |^2 &=& \sum_{\mu M_f} | C_V \langle \xi_f \, J_f \, M_f | {\pmb 1} | \xi_i \, J_i \, M_i \rangle + C_A \langle \xi_f \, J_f \, M_f | {\pmb \sigma} |\xi_i \, J_i \, M_i \rangle |^2 \\[12pt] &=& C_V^2 \sum_{\mu M_f} | \langle \xi_f \, J_f \, M_f | {\pmb 1} | \xi_i \, J_i \, M_i \rangle |^2 + C_A^2 \sum_{\mu M_f} | \langle \xi_f \, J_f \, M_f | {\pmb \sigma} | \xi_i \, J_i \, M_i \rangle |^2 \\[12pt] &=& \frac{C_V^2}{2J_i + 1} \left[ g_V^2 |(\xi_f \, J_f || {\pmb 1} || \xi_i \, J_i )|^2 + g_A^2 |(\xi_f \, J_f || {\pmb \sigma} || \xi_i \, J_i ) |^2 \right].\end{eqnarray}
$C_V$의 값은 약 $C_V/(\hbar c)^3 = 1.14984(60) \times 10^{-11} \,{\rm MeV}^{-2} $이며, 이 값은 Fermi coupling 상수 $G_F/(\hbar c)^3 = 1.16639(2) \times 10^{-11}\,{\rm MeV}^{-2}$와 비슷하기에, $C_V$ 대신 $G_F$로 쓰도록 하겠습니다. (실제로, 두 상수 값들에는 약간의 차이가 있기 때문에 보정이 필요합니다.) 또한, $g_V = 1.0$이며, $g_A = C_A/C_V$로 정의되며, 그 값은 약 1.25입니다.
그럼 위에서 주어진 각각의 행렬 성분 항들은 아래와 같이 계산 가능합니다:
\begin{eqnarray} ( \xi_f \, J_f || {\pmb 1} || \xi_i \, J_i ) = \delta_{J_i J_f} \sum_{ab} ( a || {\pmb 1} || b) ( \xi_f \, J_f || [c_a^\dagger \tilde{c}_b]_0 || \xi_i \, J_i ), \\ ( \xi_f \, J_f || {\pmb \sigma} || \xi_i \, J_i ) = \frac{1}{\sqrt{3}} \sum_{ab} ( a || {\pmb \sigma} || b) ( \xi_f \, J_f || [c_a^\dagger \tilde{c}_b]_1 || \xi_i \, J_i ). \end{eqnarray}
이 식에서 $\beta^-$ 붕괴의 경우 a는 양성자를, b는 중성자를 의미합니다. 반대로 $\beta^+$ 붕괴의 경우 $a$는 중성자, $b$는 양성자를 의미합니다.
위 행렬성분에서, Vector 항으로부터 유도된 첫번째 항의 경우, $J_i = J_f$여야 한다는 조건을 알 수 있습니다. 즉, 이 항은 Fermi transition을 의미합니다. 반면 Axial vector 항으로 부터 유도된 두번째 항의 경우, signel particle에 대한 부분을 좀 더 자세하게 계산해보면, 아래와 같이 됨을 알 수 있습니다:
\begin{eqnarray} \frac{1}{\sqrt{3}} (a || {\pmb \sigma} || b) = \sqrt{2} \delta_{n_a n_b} \delta_{l_a l_b} \hat{j}_a \hat{j}_b (-1)^{l_a + j_a + \frac{3}{2}} \begin{Bmatrix} \frac{1}{2} & \frac{1}{2} & 1 \\ j_b & j_a & l_a \end{Bmatrix} \end{eqnarray}
이 signle particle 행렬 성분 식의 결과로부터, 두번째 항은 $\Delta J = 0$ 또는 1을 허용함을 알 수 있습니다. 즉, Axial vector 성분은 Gamow-Teller transition을 의미합니다.
그럼 아래와 같이 Fermi Transition 성분을 $B_F$로, Gamow-Teller transition 성분을 $B_{GT}$로 정의하여,
\begin{eqnarray} B_F \equiv \frac{g_A^2}{2J_i + 1} |(\xi_f \, J_f || {\pmb 1} || \xi_i \, J_i )|^2, \ \ \ B_{GT} \equiv \frac{g_V^2}{2J_i +1} |( \xi_f \, J_f || {\pmb \sigma} || \xi_i \, J_i )|^2 \\[12pt] \end{eqnarray}
주어진 전이 확률 $T_{fi}$를 다시 적어보겠습니다:
\begin{eqnarray} T_{fi} &=& \frac{m_e^5 c^4}{2\pi^3 \hbar^7} f(Z, E_0) | \sum_{\mu M_f} \langle \xi_f J_f \, M_f | {\pmb O}_{\lambda \mu} | \xi_i \, J_i \, M_i \rangle |^2 \\[12pt] &=& \frac{m_e^5 c^4}{2\pi^3 \hbar^7} \left[ f(Z, E_0) G_F^2 ( B_F + B_{GT}) \right]. \end{eqnarray}
이를 이용해, 반감기 식을 아래와 같이 적을 수 있습니다.
$$ t_{1/2} = \frac{\ln 2}{T_{fi}} = \frac{2 \pi^3 \hbar^7 \ln 2}{m_e^5 c^4 G_F^2} \frac{1}{f(Z, E_0) (B_F + B_{GT})} \equiv \frac{\kappa}{f(Z, E_0) (B_F + B_{GT})} $$
여기서 $\kappa$는 아래와 같이 주어지는 상수입니다:
$$ \kappa = \frac{2 \pi^3 \hbar^7 \ln 2}{m_e^5 c^4 G_F^2} = 6147\,{\rm s}$$
그렇기 때문에, 핵의 베타 붕괴를 평가할 때, 전자에 의한 항을 왼쪽으로 넘겨, 아래와 같은 ft-값을 정의하여 많이 사용합니다:
$$ f t_{1/2} \equiv \frac{\kappa}{B_F + B_{GT}}. $$
이 값은 대체로 숫자가 크기 때문에, 아래와 같이 로그를 이용한 log-ft 값을 더 자주 씁니다:
$$ \log_{10} ft_{1/2} \equiv \log_{10} \left[ \frac{\kappa}{B_F + B_{GT}} \right]. $$
ft 값은 핵의 구조로부터 얻어지는 전이 확률 계산값에 의존하며, 위에서 보여지는 것처럼 핵의 전이 확률이 높을수록 그 값은 줄어듭니다. 예를 들면, Allowed 베타 붕괴의 경우 $\log_{10} ft_{1/2}$ 값이 2.9-10 정도 되며, 1st forbidden 붕괴의 경우 5-19 정도, 2nd forbideen decay의 경우 10-18 정도 됩니다.
다음번 포스팅에서 핵의 구조 모형을 이용해 핵에 대한 matrix element 값들을 계산해보고, 이를 이용해 반감기와 ft값을 계산해보는 작업을 포스팅 해보겠습니다.
'Nuclear Physics > From Nucleons to Nucleus' 카테고리의 다른 글
| 7장 - 베타 붕괴(Beta decay): One-Particle & One-Hole Nuclei (1) | 2024.10.20 |
|---|---|
| 7장 - 베타 붕괴(Beta Decay): Decay Branchings, Classification of allowed beta decay 등 (0) | 2024.10.19 |
| 7장 - 베타 붕괴(Beta decay): 2. Allowed Beta Decay (0) | 2024.09.12 |
| 7장 - 베타 붕괴 (Beta decay): 1. 핵 베타 붕괴의 일반적 성질 (1) | 2024.09.09 |
| 각운동량의 덧셈(2): Wigner 6j symbol (0) | 2024.05.29 |



